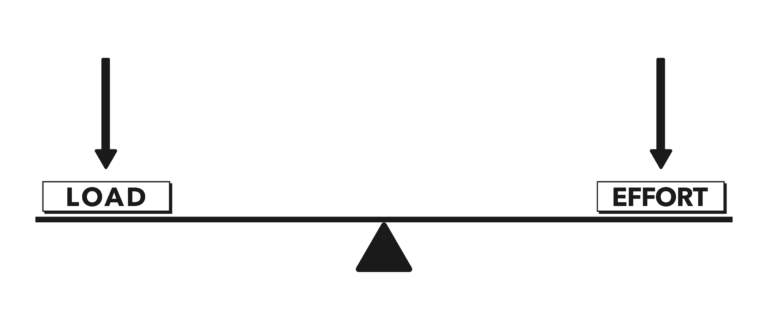
It is easy to visualize balance between load and effort in first-class levers. If the fulcrum is equidistant between the load and the effort, and if both sides have the same magnitude of force placed upon them, then the two sides balance and no movement occurs (Figure 1). We say this system is in equilibrium. We can also say that the moment (a measure of a force’s tendency to cause a body to rotate about a specific point or axis) created by each force about the fulcrum is equal to that force’s magnitude times its distance from the fulcrum. We commonly refer to the distance a force acts across a fulcrum as the moment arm.
Figure 1
In the equidistant arrangement shown in Figure 1, only the magnitude of load or magnitude of effort causes movement. This arrangement rarely occurs in anatomy, however, where it is much more common to see the fulcrum closer or further in relation to the load or effort.
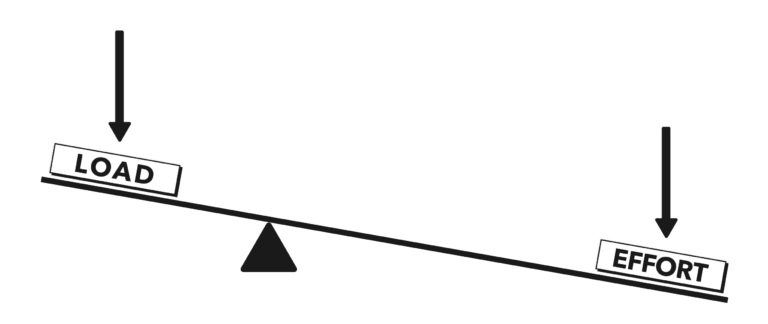
When equal forces are acting at different distances, they create different moments. Consider a case where the effort is twice the distance from the fulcrum as the load. It would create twice the moment about the fulcrum as would the load; therefore, the beam would tilt in the direction of the effort (Figure 2).
Figure 2
In our example above, the forces of load and effort are equal, and the distance of the effort is twice as far from the fulcrum as the load. We would say that the effort has twice the leverage, or mechanical advantage, as the load.
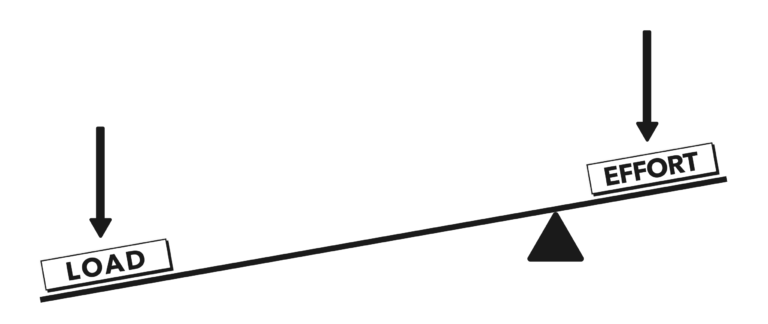
If the load and effort were of equal magnitudes, while the load was acting at three times the distance from the fulcrum than that of the effort, the moment of the load would be three times greater than that of the effort. The beam would tilt in the direction of the load; it has three times the leverage (Figure 3).
Figure 3
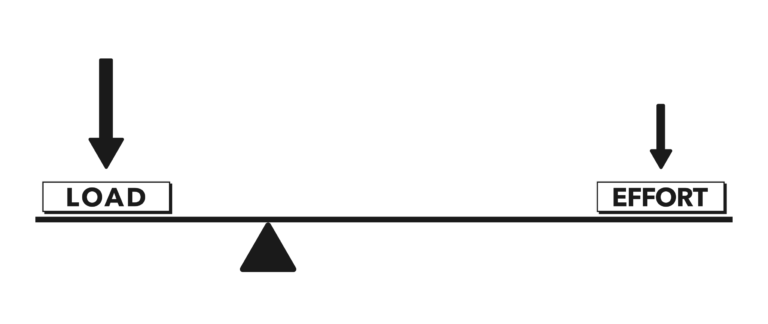
Ultimately, the further a force is applied from a fulcrum, or pivot point, the greater its magnitude (advantage) is multiplied.
With this same concept, we can see how halving a force while doubling its distance could be advantageous in creating efficiency (Figure 4).
Figure 4
As we consider other classes of levers, we should keep in mind that the direction of lever movement is dependent on moment rather than absolute force produced by the muscle or absolute load applied.
For a condition of equilibrium and no movement:
Force of the load x distance from the fulcrum = force of the muscular effort x distance from the fulcrum
For a movement in the direction of effort:
Force of the load x distance from the fulcrum < force of the muscular effort x distance from the fulcrum
For a movement in the direction of the load:
Force of the load x distance from the fulcrum > force of the muscular effort x distance from the fulcrum
Anatomy of Levers, Part 2: Leverage and Moments